La coincidencia matemática del año 2025

El año 2025 trajo consigo una coincidencia matemática única y fascinante. Además de ser un cuadrado perfecto, ya que 45² (45 x 45) da como resultado 2025, también presenta una curiosa suma de cubos. 2025 es igual a la suma de los cubos de los primeros nueve números enteros consecutivos: 1³ + 2³ + 3³ + 4³ + 5³ + 6³ + 7³ + 8³ + 9³, que también es exactamente 2025.
Esta relación matemática es rara y no se ha producido desde el año 1296, y no se repetirá hasta el año 3025. La idea de que 2025 puede expresarse como el cuadrado de 45 o como la suma de los cubos de números consecutivos añade una capa desde la complejidad y la belleza hasta las matemáticas, mostrando cómo ciertos números tienen propiedades que los hacen especiales y únicos.
Coincidencias como ésta, que involucran tanto operaciones simples como conceptos más complejos, son siempre un deleite para los matemáticos. Nos recuerdan que los números, incluso en su forma más simple, están llenos de sorpresas y relaciones inesperadas. El año 2025 estará marcado, pues, por esta intrigante peculiaridad matemática, que nos hará mirar los números de una manera nueva y fascinante.
El origen del símbolo de la igualdad

El símbolo de igualdad (=), utilizado universalmente en matemáticas y en diversas áreas del conocimiento, tiene un origen que se remonta a más de 450 años. Creado por el matemático inglés Robert Recorde en 1557, el símbolo surgió de una idea simple pero poderosa: "no pueden haber dos cosas más iguales que dos líneas paralelas". Esta frase fue la inspiración de Recorde para crear el símbolo que, hasta el día de hoy, usamos para indicar que dos expresiones tienen el mismo valor.
Antes de la invención del símbolo de igualdad, las ecuaciones se expresaban de forma más verbal, lo que hacía que los cálculos fueran más complicados. Recuerde, cuando buscaba una manera de simplificar la notación matemática, creó un símbolo que pudiera representar clara y rápidamente esta relación de igualdad. La elección de dos líneas paralelas refleja la idea de equilibrio y simetría, conceptos fundamentales en las operaciones matemáticas.
El símbolo de igualdad fue introducido en su obra La piedra de afilar de Witte y, con el tiempo, fue ampliamente adoptado por la comunidad matemática. Hoy en día, es uno de los símbolos más reconocidos en el mundo, no sólo en matemáticas, sino también en áreas como la lógica, la programación y la ciencia en general, siendo esencial en la construcción y solución de ecuaciones y fórmulas.
Elija un Desafíos de Quiz
Descubre algunos datos interesantes sobre Matemáticas
El desafío infinito que conquistó el mundo

El cubo de Rubik, creado por el arquitecto y profesor de arquitectura húngaro Ernő Rubik en 1974, se ha convertido en uno de los rompecabezas más populares del mundo y en un auténtico icono cultural. Rubik lo inventó originalmente como una herramienta de enseñanza para enseñar a sus estudiantes sobre geometría y transformaciones espaciales, pero pronto se convirtió en un desafío mundial.
El cubo 3x3x3, la versión más conocida, tiene alrededor de 43 trillones de combinaciones posibles (43.252.003.274.489.856.000), pero sólo una solución única. Esta impresionante cantidad de posibilidades refleja la complejidad del cubo y por qué ha fascinado a tanta gente a lo largo de los años. A pesar de su dificultad, el Cubo de Rubik también ha generado un fenómeno global llamado "speedcubing", donde los competidores intentan resolver el cubo lo más rápido posible. El récord actual para resolver el cubo 3x3x3 es de 3,13 segundos, una hazaña impresionante que demuestra la habilidad y la práctica que implica este arte.
Además del modelo clásico, el Cubo de Rubik ha inspirado numerosas variaciones. Hay cubos con tamaños mayores, como 4x4x4, 5x5x5 e incluso versiones más complejas, como el cubo 11x11x11. Estas variaciones aumentan significativamente la complejidad y el número de combinaciones, proporcionando desafíos aún mayores para los entusiastas.
El misterio del símbolo del infinito

El símbolo de infinito (∞) es ampliamente reconocido en áreas como las matemáticas, la filosofía y otras ciencias, estando asociado a la idea de algo que no tiene fin. Su origen se remonta al siglo XVII, cuando el matemático inglés John Wallis la introdujo en su obra Arithmetica Infinitorum, en 1656, para representar una cantidad infinita. Sin embargo, Wallis nunca explicó claramente por qué eligió este símbolo, lo que ha dado lugar a algunas teorías sobre su origen.
Una de las explicaciones más aceptadas es que Wallis se inspiró en el símbolo romano del número mil, “CIƆ”, utilizado en la antigua Roma para representar grandes cantidades. Otro dato interesante es que el símbolo del infinito también es conocido como lemniscata, que proviene del latín lemniscatus, que significa “decorado con cintas”. Este término está relacionado con una curva geométrica, el "ocho", que estudiaron matemáticos como Jakob Bernoulli y que representa el concepto de algo sin fin.
Además de utilizarse en matemáticas, el símbolo también aparece en filosofía, para expresar ideas de eternidad y tiempo infinito, y en astronomía, en curvas como el "anillo", que representa la trayectoria del sol a lo largo del año. #
Con el tiempo, el símbolo se hizo popular y se convirtió en un elemento esencial en la notación matemática, ayudando a expresar conceptos como la continuidad y los límites.
23 de noviembre día de Fibonacci

23 de noviembre día de Fibonacci . Se eligió la fecha porque, al referirse a la secuencia de Fibonacci, que es una serie numérica en la que cada número es la suma de los dos anteriores (0, 1, 1, 2, 3, 5, 8, 13, 21, etc. ), la secuencia puede representarse por el par de números (1, 1) el día 23 de noviembre, si consideramos los números 23 y 11. El origen de la celebración se remonta al matemático italiano Leonardo de Pisa, conocido como Fibonacci, quien Vivió en el siglo XIII. Es famoso por introducir la secuencia de Fibonacci en el mundo occidental a través de su libro Liber Abaci, publicado en 1202. La secuencia no sólo aparece en varias áreas de las matemáticas, sino que también se manifiesta en patrones naturales, como la disposición de las hojas de una planta. , en reproducción de conejos y en estructuras florales.
celebrar 23 de Noviembre
El 22 de julio se celebra el Día de Aproximación de Pi

El 22 de julio se celebra el Día de Aproximación de Pi , también conocido como Día de Aproximación de Pi o Día de Pi Aproximado. Esta fecha es una referencia al valor aproximado de Pi (π), que a menudo se redondea a 3,14. Pi es una constante matemática que representa la relación entre la circunferencia de un círculo y su diámetro. El valor de Pi es una secuencia infinita y no repetida de dígitos decimales, y su aproximación a 3,14 se utiliza a menudo en cálculos y problemas matemáticos. El Día de la Aproximación de Pi es una oportunidad para celebrar la importancia de esta constante matemática y su aplicación en diversas áreas de la ciencia y la ingeniería.
celebrar 22 de Julio
Sustracción

Sustracción. Propiedades
39 - 28 = 11 (Se lee: La diferencia entre treinta y nueve y veintiocho es igual a once.)
39 (Suma), 28(Resta) y 11(Diferencia)
Nota : Para comprobar si la resta se realiza correctamente se puede aplicar la propiedad fundamental de la resta:
La suma de la resta y la diferencia es igual al aditivo.
Para hacer una estimación de una diferencia, normalmente redondea los números a las decenas o centenas más cercanas.
903 + 288 = 615 (Valor exacto)
900 - 300 = 600 (Estimación)
Suma

Suma. Propiedades
30 + 11 = 50 (léase: La suma de treinta y nueve y once es igual a 50.)
39 y 11 son las cuotas y 50 es la suma.
Propiedades de la suma:
- Conmutativo: a + b = b + a
Cambiando el orden de las cuotas la suma no cambia.
39 + 11 = 11 + 39 = 50
- Asociativo: (a + b) + c (b + c)
La suma no cambia al asociar las cuotas de forma diferente.
(39 + 11) + 28 = 39 + (11 + 28) = 78
- Existencia de elementos neutros : a + 0 = 0 + a = a
o (cero) es el elemento neutro de la suma.
Para hacer una estimación de una suma, normalmente redondeamos los números a las decenas o centenas más cercanas.
39 + 11 + 28 = 78 (Valor exacto)
40 + 10 + 30 = 80 (Estimado)
Un conjunto es una colección de elementos distintos

Un conjunto es una colección de elementos distintos agrupados en una sola entidad. Los elementos pueden ser números, objetos, personas o cualquier cosa que pueda identificarse de forma única. Los conjuntos se representan entre llaves {}. Algunos conceptos importantes relacionados con los conjuntos incluyen: Pertenencia: un elemento puede pertenecer a un conjunto. Si un elemento está presente en un conjunto, se dice que pertenece a ese conjunto. Conjunto vacío: Es un conjunto que no tiene elementos. Subconjunto: Un conjunto se considera subconjunto de otro conjunto si todos sus elementos también pertenecen al conjunto mayor. Unión: La unión de dos conjuntos es un conjunto nuevo que contiene todos los elementos de los conjuntos originales, sin repeticiones. Intersección: La intersección de dos conjuntos es un nuevo conjunto que contiene solo los elementos comunes a ambos conjuntos.
Una ecuación de primer grado es una ecuación polinomial cuyo mayor grado es 1
Una ecuación de primer grado es una ecuación polinomial cuyo mayor grado es 1. Se expresa en la forma general: ax + b = 0, donde a y b son constantes conocidas yx es la variable desconocida. La solución de una ecuación de primer grado es un valor específico de x que hace verdadera la igualdad. Para resolver la ecuación: Aislamiento del término con la incógnita: Pasar el término que contiene la variable a un lado de la ecuación, para que quede solo. Todos los demás términos se trasladan al otro lado. Simplificación de la ecuación: Realiza las operaciones matemáticas necesarias para simplificar la ecuación. Aislamiento de variables: divida ambos lados de la ecuación por el coeficiente de x para aislar la variable. Solución de la ecuación: Obtenga el valor de x que hace verdadera la igualdad, llamada solución de la ecuación. Una ecuación de primer grado tiene solución única, a menos que sea una ecuación de identidad, donde cualquier valor de x satisface la igualdad.
Una ecuación cuadrática, o ecuación cuadrática

Una ecuación cuadrática, o ecuación cuadrática, es una ecuación polinomial con el mayor grado igual a 2. Se representa en la forma general: ax^2 + bx + c = 0, donde a, b y c son constantes y x es la variable desconocida. Hay tres posibles tipos de soluciones para una ecuación cuadrática: Dos raíces reales y distintas: Cuando el discriminante (∆) de la ecuación es mayor que cero (∆ > 0), la ecuación tiene dos raíces reales diferentes. Dos raíces reales e iguales: Cuando el discriminante es igual a cero (∆ = 0), la ecuación tiene dos raíces reales iguales, dando como resultado una solución única. Sin raíces reales: Cuando el discriminante es menor que cero (∆ < 0 ), la ecuación no tiene raíces reales. En este caso, las raíces pueden ser números complejos conjugados.
O famoso livro de Malba Tahan, “O Homem que Calculava”

O famoso livro de Malba Tahan, “O Homem que Calculava”, descreve uma teoria conhecida como “quatro quatros”. Esta técnica permite a formação de qualquer número inteiro entre 0 e 100 usando apenas quatro numerais 4 e sinais de operações matemáticas. Por exemplo, para obter um “3”, basta efetuar a operação (4+4+4)/4.
O número de ouro é uma teoria matemática fascinante e que está cercada de mitos

O número de ouro é uma teoria matemática fascinante e que está cercada de mitos. Representado pelo símbolo grego Phi (f), esse número, 1,6180, é a razão diagonal/lado de um pentágono regular e foi estudado desde a Antiguidade. Ele indica harmonia, motivo pelo qual está presente em obras de Leonardo da Vinci, em construções como as Pirâmides do Egito e até no tamanho das falanges humanas.
Enquanto muitos jovens nos dias atuais buscam diversão em

Enquanto muitos jovens nos dias atuais buscam diversão em jogos de videogame ou atividades esportivas, Evariste Galois optou por um caminho diferente: aprofundar seus estudos na Matemática. Considerado um dos mais brilhantes pensadores da área científica, Galois chegou a desafiar os professores e preferir os livros de gênios consagrados ao invés das aulas. Apesar de ter deixado apenas 60 páginas de anotações, o seu legado foi considerado fundamental para o desenvolvimento da Matemática. Tragicamente, a sua vida teve um fim prematuro, pois, em 1832, Galois defendeu a honra de uma forma trágica: tomou uma pistola e morreu em um duelo.
O professor mandou que seus alunos somassem todos os números de um a cem

O professor mandou que seus alunos somassem todos os números de um a cem, e ficou surpreso ao ver que o jovem Gauss conseguiu a resposta correta, 5.050, em poucos segundos. O que fez o menino perceber essa conta tão rapidamente foi a sua capacidade de observar e calcular que, se somasse o primeiro número com o último, 1 + 100, obtinha 101. Ao somar o segundo número com o penúltimo, 2 + 99, o resultado também foi 101. Então, Gauss descobriu que somar todos os números de um a cem equivalia a somar 50 vezes o número 101, o que resulta em 5.050. Essa foi a primeira vez que ele inventou a fórmula da soma de progressões aritméticas, ainda criança. Gauss, que viveu entre 1777 e 1855, é considerado por muitos como o maior gênio matemático de todos os tempos, e por isso é conhecido como o Príncipe da Matemática.
Aproximadamente 8 x 10^67 maneiras diferentes podem ser

Aproximadamente 8 x 10^67 maneiras diferentes podem ser usadas para classificar um baralho de cartas. Para colocar isso em perspectiva, mesmo que alguém vire um baralho de cartas a cada segundo desde o início do universo, ainda assim seria impossível encontrar uma repetição antes do universo chegar ao fim.
Não é possível pentear todos os pelos de uma bola de tênis na mesma direção
Não é possível pentear todos os pelos de uma bola de tênis na mesma direção. Esse problema matemático é conhecido como o teorema de Henri Poincaré. Ele foi formulado no final do século XIX e pode ser matematicamente descrito como "não há campo vetorial tangente contínuo não desaparecendo em n-esferas de dimensão par". No entanto, é mais facilmente expressado como "você não pode pentear uma bola peluda sem criar um topete". Este teorema foi confirmado por Brouwer em 1912, e tem uma consequência interessante: em um planeta esférico ideal, há pelo menos um ponto em que o vento está soprando. O planeta não precisa ser perfeitamente esférico, mas deve ser contínuo - o que significa que não deve ter buracos ou saliências no meio.
O número pi é encontrado em todos os lugares

O número pi é encontrado em todos os lugares. Seu envolvimento com círculos é bem conhecido, mas também surge em outros cenários. Por exemplo, a série 1/1 2 + 1/2 2 + 1/3 2 + 1/4 2 + 1/5 2 … = 1 + 1/4 + 1/9 + 1/16 + 1/25 ... aproxima-se cada vez mais do valor π2 / 6 = 1,645... à medida que mais e mais termos são adicionados. Ao inverter essa fração, obtemos 6/π2, que é igual à probabilidade de que dois números, desde que sejam grandes o suficiente, sejam primos - ou seja, que não tenham fatores comuns além de 1.
A Matemática nos oferece uma curiosa descoberta

A Matemática nos oferece uma curiosa descoberta, conhecida como Chifre de Gabriel. Esta superfície é formada pela rotação da curva y = 1/x, uma hipérbole retangular, em torno do eixo x para valores maiores que um. O notável fato descoberto pelo físico e matemático italiano Evangelista Torricelli é que, apesar de o Chifre ter um volume finito, igual a π unidades cúbicas, a área de sua superfície é infinita. Se o Chifre fosse preenchido com tinta, não haveria quantidade suficiente para cobrir toda a sua área.
A Sequência de Fibonacci é famosa por ser encontrada na natureza

A Sequência de Fibonacci é famosa por ser encontrada na natureza. O processo para criar a sequência é somar dois números inteiros anteriores para gerar o próximo. Por exemplo, começando com 0 e 1, a sequência se desenvolve assim: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, etc. Esta sequência foi descoberta durante um experimento sobre o crescimento de coelhos. Além disso, a música "Lateralus" da banda americana de prog metal Tool é composta seguindo a sequência Fibonacci.
Os algarismos romanos
Os algarismos romanos foram originariamente desenvolvidos para fins de negociação. Eles foram amplamente usados em todo o Império Romano para fins contábeis, permitindo que os romanos façam transações rápidas com produtos e serviços. Após a queda do Império Romano, essa forma de numeração foi adotada por toda a Europa. No entanto, ela foi gradualmente substituída por outros sistemas de numeração a partir do século XVI.
Sabemos o que é ano-luz
Sabemos o que é ano-luz: uma unidade de comprimento que indica a distância percorrida pela luz em um ano. A luz desenvolve uma velocidade de 300.000km/s, o que significa que, em um segundo, ela percorre 300.000km. Logo, em um ano, ela percorre 9.460.800.000.000Km, mais de 9 trilhões de quilômetros! Quando alguém afirma que uma galáxia está a 10 anos-luz de distância da Terra, isso significa que ela se encontra a uma distância de 90 trilhões de quilômetro
Notou-se que as cadeiras com quatro pés costumam apresentar desequilíbrio

Notou-se que as cadeiras com quatro pés costumam apresentar desequilíbrio, enquanto as de três pés não. A matemática explica esse fato, mas é algo de complicada compreensão. Para compreender o porquê, observe a porteira de uma fazenda. Ela conta com uma tábua na diagonal, formando dois triângulos. Dessa forma, ela é mais resistente à deformação e a manutenção de seu equilíbrio é garantida. Da mesma forma, os três pés de uma cadeira formam um triângulo, tornando-a mais robusta e estável.
Por que escrevemos os números da forma que conhecemos? Se
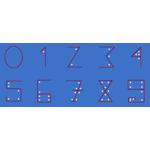
Por que escrevemos os números da forma que conhecemos? Se você achou que alguém simplesmente decidiu que seria assim, está enganado! Por trás dessa escrita existe uma explicação. Cada um dos números entre 0 e 9 foi criado com base no número de ângulos que ele possui. Por exemplo, o número 3 é representado por um símbolo com 3 ângulos. Confira na representação ao lado.
Desde a Antiguidade

Desde a Antiguidade, os números vêm sendo usados para a contagem de objetos e animais. O povo egípcio foi um dos primeiros a criar um sistema de numeração, no ano de 3.000 a.C. Outros povos também foram criando seus próprios métodos de contagem, como os romanos, que criaram os números romanos, que são usados até hoje para relógios, livros e na contagem dos séculos. Porém, o sistema de numeração que usamos hoje foi criado pelos indianos, no Norte da Índia, no século V.
O número 1089 é conhecido como número mágico

O número 1089 é conhecido como número mágico. Para obtê-lo, escolha um número com três dígitos diferentes, como por exemplo 683. Escreva o número que escolheu e subtraia-o de trás para frente: 723 -327 = 396. Por fim, pegue o resultador e some-o de trás para frente: 396 + 693 = 1089, o que totaliza 1089. Esse cálculo funciona com qualquer número de três dígitos.
Existe um cálculo matemático de 4 etapas que resultará sempre no número 6

Existe um cálculo matemático de 4 etapas que resultará sempre no número 6. Vamos lá, o primeiro passo é: (1) Pense em um número, por exemplo: 104; (2) Multiplique-o por 2: 104 x 2 = 208; (3) Agora some 12 no valor: 208 + 12 = 220; (4) O próximo passo é dividir o resultado por 2: 220 / 2 = 110; (5) E por fim, pegue o valor obtido no cálculo e subtraia o número inicial: 110 – 104 = 6. A explicação por trás desse resultado dar sempre 6 está na álgebra.
El 14 de marzo se celebra el Día Internacional de las Matemáticas

El 14 de marzo se celebra el Día Internacional de las Matemáticas , conocido como Día de Pi debido a la representación numérica de la fecha (14/3), que corresponde a los primeros dígitos del número pi. A partir de 2020, por decisión de la UNESCO, se comenzó a reconocer oficialmente el día para celebrar la importancia de las matemáticas en todo el mundo. Cada año tiene un tema específico y las celebraciones incluyen una variedad de eventos y actividades educativas para promover el interés y la comprensión de las matemáticas.
celebrar 14 de Marzo
Volver









